Author | Created | Updated |
mcha(Min-jae Cha) | 2021. 12. 20 | 2022. 01. 08 |
진짜 엄청 오래 걸린 과제. 집중도 안한 것도 있지만 문제를 제대로 이해하지 않고 진행 한 것도 정말 문제
0. Intro
push_swap은 과제에서 제시한 제한된 명령어를 사용하여 스택 A와 스택 B를 정렬하는 과제이다.
정렬 방식은 사람마다 다 다르고 무한하지만 입력 받는 인자의 개수에 따라 사용할 수 있는 명령어 수가 어느 정도 정해져 있다.
따라서 효율적인 정렬 방법을 사용하지 않으면 좋은 점수를 받지 못하거나 KO를 받을 수 있다.
중요한 부분은 내가 설계한 정렬 알고리즘을 통해 프로그램이 알아서 정렬을 한다는 것이다.
따라서 다양한 유형의 정렬 알고리즘을 분석하고 사용하고 재구성하여 이 프로그램에 효율적인 정렬 알고리즘을 제시해야 한다.
1. Error Type
→ a 에 들어오는 값이 중복인지
→ a 에 들어오는 값이 int 범위 내에 있는지
→ a 에 들어오는 값이 숫자인지
 Duplicate check - Memoization
Duplicate check - Memoization
a 스택에 들어오는 값들은 중복되면 안된다. 예를 들어 a에 [ 1, 2, 3, 1, 4 ] 의 다섯 개의 값이 들어온다고 했을 때 1이 중복되어 들어오기 때문에 Error로 판단하여 처리해야 한다.
이러한 중복을 판단하는 방법은 크게 세 가지가 있다고 판단하였다. 받아온 배열의 모든 값을 하나하나씩 검사하여 중복 여부를 검사하는 방법인 Brute Force, 들어온 인자를 메모리에 저장하여 검사하는 Memoization, 이진 트리 방식을 개선한 Red-Black Tree 가 있다. 이 중 가장 효율적인 방법은 Red-Black Tree 방법이지만 이해도와 지식이 부족하여 Memoization을 사용한다.
Memoization 은 동일한 작업을 반복해야 할 때 이전에 계산한 값을 메모리에 저장하여 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술이다.
Memoization 방식을 사용한다고 했을 때 가장 곤란한 부분은 효율적인 메모리 사용이 불가능하단 점이었다.
예를 들어 1, 2, 3, 4, 5 의 값이 들어오게 된다면 다섯 개의 배열만을 할당하여 효율적으로 중복 체크를 할 수 있지만, 만약 -1000000, 1, 2, 3, 4, 5 값이 들어오게 된다면 -1000000을 위해 매우 많은 메모리를 추가적으로 할당해주어야 한다는 단점이 있다.
2. Data Structure
 스택(Stack)
스택(Stack)
스택은 제한적으로 접근이 가능한 자료구조이다.
제한적으로 접근이 가능하다고 하는 이유는 한 쪽 끝에서만 접근이 가능하기 때문이다.
한 쪽 끝에서만 자료를 넣고 뺄 수 있는 스택은 선형 구조(LIFO - Last In First Out, 후입선출)로 되어있다.
스택의 동작은 자료를 넣는 행위인 Push와 자료를 빼는 행위인 Pop으로 구성되어 있다.
자료를 넣은 후 사용하고자 할 때 Pop의 결과인 꺼낸 자료는 가장 최근에 넣은 자료이다.
넣은(Push) 순서 | 1 | 2 | 3 | 4 |
넣은 자료 | A | B | C | D |
꺼낸(Pop) 순서 | 1 | 2 | 3 | 4 |
꺼낸 자료 | D | C | B | A |
위의 예를 보면 A→B→C→D 순서로 스택에 자료를 넣은 뒤, 다시 이 자료를 꺼낸다고 할 때
넣은 순서인 A→B→C→D 순서 그대로 꺼낼 수 있는 것이 아닌 가장 최근에 넣은 자료부터 D→C→B→A 순서로 데이터를 꺼낼 수 있다.
 큐(Queue)
큐(Queue)
큐는 스택(Stack)과는 반대 되는 개념을 가진 자료구조로 선입선출(FIFO - Frist In First Out) 구조로 데이터를 저장한다.
큐는 데이터를 넣는 행위인 Put(Insert)와 데이터를 꺼내는 행위인 Get(Delete)로 구성 되어 있다.
어느 물건을 사기 위해 줄을 서있다고 생각했다. 줄을 A→B→C→D 순서로 서있다.
이 때, 스택처럼 제일 나중에 들어온 사람인 D가 먼저 물건을 살 수 있지 않고, 먼저 온 사람인 A가 제일 먼저 물건을 살 수 있는 기회를 갖게 된다.
넣은(Put) 순서 | 1 | 2 | 3 | 4 |
넣은 자료 | A | B | C | D |
꺼낸(Get) 순서 | 1 | 2 | 3 | 4 |
꺼낸 자료 | A | B | C | D |
데이터의 위치를 가리키는 Front(head)와 Rear(tail)은 각각 데이터를 Get(Delete) 할 수 있는 위치와 데이터를 Put(Insert) 할 수 있는 위치를 가리킨다.
용어 | 설명 |
Front(Head) | 데이터를 Get 할 수 있는 위치 |
Rear(Tail) | 데이터를 Put 할 수 있는 위치 |
큐의 종류에는 크게 선형 큐와 환형 큐가 있다.
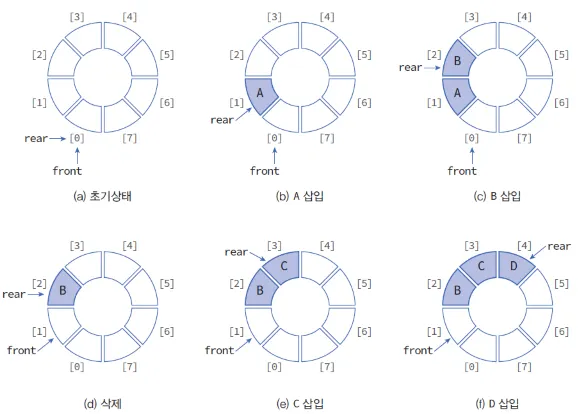
 선형 큐
선형 큐
선형 큐는 막대 형태로 되어 있는 큐로 일반적인 큐의 형태를 나타낸다.
큐(Queue)는 데이터를 Get할 수 있는 Front와 데이터를 Put 하는 Rear의 위치와 관계에 따라 큐의 데이터 수용 여부를 판단한다.
주어진 큐의 크기를 N이라고 했을 때 rear가 N-1을 가리키고 있으면 그 큐는 꽉 찬 것이라고 인식한다.
if (rear == N-1) -> (Queue is Empty)
C
복사
만약 front와 rear가 같다면 큐가 비어있다고 판단한다.
if (front == rear) -> (Queue is Full)
C
복사
하지만 5개의 공간이 주어지고 각 공간에 A, B, C, D, E라는 데이터를 넣은 뒤 A, B, C, D를 Get하여 사용하면 그 다음의 큐는 E 만 남아있는 상태임에도 불구하고 꽉 찬 큐라고 인식한다.
→ A, B, C, D, E를 큐에 넣었을 때
front | rear | |||
A | B | C | D | E |
→ A, B, C, D를 큐에서 꺼냈을 때
front, rear | ||||
E |
큐에서 데이터를 Get 했을 때 남아 있는 데이터의 위치를 한 칸씩 앞으로 이동시키지 않고 인덱스 단위로 큐의 연산을 수행했기 때문이다.
따라서 선형 큐를 옳게 사용하기 위해서는 빈 공간을 사용하기 위해 모든 자료를 꺼내고 다시 삽입하거나, 모든 자료를 한 칸 씩 옮겨야 한다는 단점이 있다.
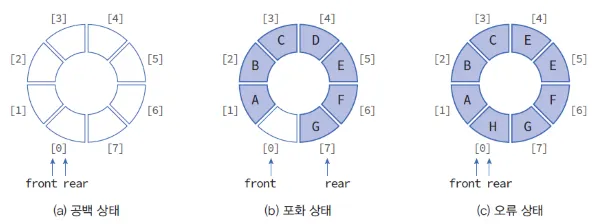
 환형 큐
환형 큐
환형 큐는 선형 큐의 단점을 보완한 구조이다.
front가 큐의 끝에 닿으면 큐의 맨 앞으로 자료들을 보내어 원형으로 연결 하는 방식이다.
처음과 끝이 원형처럼 이어져 있다고 생각하면 쉽다.
기본적인 작동 방식은 다음과 같다.
자료를 Get 할 수 있는 front와 rear를 초기화 한 뒤, 데이터를 하나씩 넣을 때마다 rear의 위치를 1씩 증가시킨다.
마찬가지로 데이터를 하나씩 꺼낼 때에는 front의 위치를 1씩 증가시킨다.
선형 큐와 달리 환형 큐의 공백 상태는 front와 rear의 위치가 같을 때를 말한다.
그림에서 볼 수 있듯이 큐의 모든 공간이 자료로 꽉 차 있으면 오류 상태로 인식한다.
따라서 정상적인 환형 큐를 운영하기 위해서는 front의 위치는 항상 비어있어야 한다. 다시 말해 환형 큐의 적어도 한 공간은 빈 상태로 유지해야한다.
공백 상태의 반대인 포화 상태도 마찬가지로 front와 rear의 관계를 통해 판단한다.
공식은 front == (rear + 1) % QUEUE_SIZE이다.
 덱(Deque)
덱(Deque)
덱, 데크라고 불리는 자료구조는 위에서 설명한 큐가 응용된 형태이다.
큐는 front에서 자료를 꺼낼 수 있고 rear에서 데이터를 넣을 수 있는 단방향(One-way) 구조이다.
하지만 덱(Deque)는 Double-ended queue의 줄임말로 큐와 달리 양방향으로 데이터를 넣고 뺄 수 있다.
 고찰
고찰
진행 중인 과제인 push_swap 문서 내에 수행할 수 있는 연산의 종류에 대한 항목이 있다.
주어진 a와 b의 top에 있는 두 원소의 위치를 바꾸는 swap, 데이터를 넣는 push가 있는데 특별한 부분은 바로 rotate 부분이다.
rotate 연산의 특징을 살펴보면 각 자료구조의 탑에 있는 원소를 가장 뒤에 넣고 안에 있는 원소들의 위치의 인덱스를 1만큼 앞으로 이동시킨다. 반대로 제일 마지막에 있는 원소를 제일 위로 올리고 인덱스를 1만큼 뒤로 움직이는 reverse rotate 도 존재한다.
이렇게 원소들을 회전하는 연산을 수행할 때 스택을 사용하려면 곤란한 상황이 펼쳐질 것이라고 생각하였다.
따라서 삽입 삭제가 양쪽에서 가능한 덱(Deque)을 사용하여 구현하는 것이 가장 가깝다고 생각하였다.
3. Sorting Algorithm
알고리즘은 어떤 목적이나 목표를 달성하기 위해 수행해야 하는 일련의 과정들을 말한다.
A부터 B까지 가는 방법 즉, 알고리즘은 매우 다양하며 그 방법에 따라 소요되는 시간과 노력 또한 상이하다.
A에서 B로 갈 때 주위 풍경을 둘러보며 여유롭게 힐링을 하며 가는 것도 좋다.
하지만 프로그래밍 에서는 가장 효율적인, 빠른 방법을 찾아 문제를 해결해야 한다.
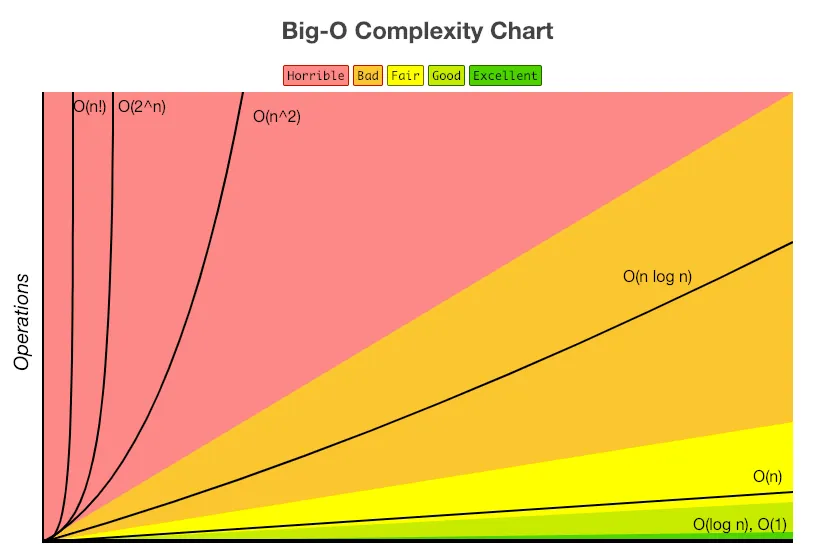
가장 빠른 방법과 관련된 것은 시간 복잡도인데, 이 시간 복잡도(Time Complexity)는 프로그램에 들어오는 입력(input, N)의 크기에 따라 실행되는 연산의 수를 말한다.
알고리즘의 실행 시간은 컴퓨터의 하드웨어 사양, 사용된 언어 종류, 컴파일러의 속도 등에 따라 다르다고 말한다.
알고리즘의 실행 시간에서 집중해야 할 부분은 입력 값에 따른 함수의 증가량인 성장률이다.
점근적 표기법(Asymptotic notation)은 가장 큰 영향을 주는 항만 계산하는 방법인데, 종류는 아래와 같이 크게 세 가지가 있다.
최상의 경우 | 오메가 표기법 (Big-Ω Notation) |
평균의 경우 | 세타 표기법 (Big-θ Notation) |
최악의 경우 | 빅오 표기법 (Big-O Notation) |
사용하면 가장 정확하고 좋은 세타 표기법은 평가하기가 까다로워 제일 최악의 경우에 사용하는 빅오 표기법을 사용한다.
그 이유는 알고리즘이 최악일 때의 경우를 판단하면 평균과 가까운 성능으로 예측하기 쉽다고 한다.
 빅오 표기법 (Big - O)
빅오 표기법 (Big - O)
 정렬 알고리즘에 따른 시간 복잡도
정렬 알고리즘에 따른 시간 복잡도
Algorithms | 최선 | 평균 | 최악 |
Bubble | |||
Heap | |||
Insertion | |||
Merge | |||
Quick | |||
Selection | |||
Shell | |||
Smooth |
 퀵 정렬(Quick-sort)
퀵 정렬(Quick-sort)
퀵 정렬은 나열 된 수 중 기준이 되는 임의의 수인 Pivot을 선정하고, 해당 Pivot을 기준으로 작거나 같은 수를 왼쪽 파티션, 큰 수를 오른쪽 파티션으로 보낸다.
그 뒤에 나누어진 왼쪽과 오른쪽 파티션 각각에서 다시 한 번 Pivot을 선정한 후 위의 과정을 반복 진행한다.
퀵 정렬의 핵심은 기준이 되는 수인 이 Pivot을 적절하게 선정하는 것인데, 만약 선정한 수가 최댓값 또는 최솟값이라면 시간 복잡도가 O()이 된다.
퀵 정렬의 최선 시간 복잡도인 O()을 보장하기 위해서는 나열 된 수의 중앙 값 또는 그와 근사한 값을 선정해야 한다. 하지만 그 중앙 값을 찾기 위해서 가장 빠른 방법은 나열된 수를 한 번 정렬 한 뒤 그 정렬 된 수열의 중앙에 있는 값을 Pivot으로 선정하는 것이다.
이런 비 효율적인 방법이 없을 수 없다.
하지만 이 방법을 사용하였다. ( 2022. 01. 08 )
4. Process
처음 생각 한 방법은 스택 A와 스택 B에서 작업을 할 때 퀵 소트를 바탕으로 해서 정렬을 하는 것이었다.
위에서 언급한 바와 같이 퀵 소트에서 가장 중요한 것은 시간 복잡도가 극적으로 나빠지는 것을 막는 것이다.
따라서 바람직한 피봇(Pivot)을 선정하는 것이 가장 중요하였는데, 정렬이 안 된 리스트를 한 번 정렬 한 다음에 그 중에서 피봇을 선정하는 것은 시간이 배로 든다고 생각하였다.
따라서 각각의 스택에서 작업해야 하는 인자의 개수에 따라 식을 세워 대충 중간 ‘위치'에 있는 수를 피봇으로 선정하였다.
나름 쓸만한 방법이라고 생각하였지만 이 방법은 옳지 않았고, 결국에는 차라리 리스트를 정렬한 후에 피봇을 선정하는 것이 더 바람직하였다.
이 방법은 피봇을 한 개만 선정해서 작업을 하는 방식이었는데, 일정 개수 만큼 남을 때 까지 분할을 계속하여 시간과 명령 수행 횟수가 너무 많아졌다.
다음은 위에 적어둔 push_swap 가이드를 보고 배운 부분을 적용하였다.
인자 개수가 5개일 때, 그리고 3개 이하일 때에는 따로 예외 처리를 하여 직접 정렬을 해주는 방법이 더 빨랐다.
이 외 개수의 인자를 받을 경우 피봇을 2개 설정하여 정렬하는 것도 도움이 되었다.
→ 작성한 pseudo-code
→ 인자가 4개일 때의 경우
1개, 2개, 3개, 5개의 인자를 처리 할 때 따로 예외로 걸러내어 처리를 하였을 때 기존의 것 보다 좋은 결과를 얻어냈다. 하지만, 테스터기를 통해 검사를 했을 때 4개의 인자를 처리 할 경우 좋은 효율을 얻지 못해 Fail을 받았다.
적용한 알고리즘의 핵심은 얼마나 적은 수의 그리고 얼마나 큰 값들을 스택 A에 남겨두냐, 그리고 얼마나 적게 명령어를 사용하는가 였다.
그 후 작은 값들이 모여져 있는 스택 B에서 내림차순으로 정렬을 하여 A로 옮겨야 했다.
만약 인자가 4→2→3→1이 주어져 있는 경우 수정 전의 피봇을 알고리즘에 의하면 2하고 1이 피봇이 되었다.
이 경우 A에 남아있어야 하는 4와 3에 대해 연산이 많이 이루어지기 때문에 효율성이 좋지 않아 다음과 같이 수정하였다.
1.
내림차순으로 정렬하기
4→3→2→1
2.
앞에 있는 두 개의 수를 피봇으로 선정하기
Pivot 1 : 4
Pivot 2 : 3
3.
큰 피봇과 작은 피봇 선정하기
Big Pivot : 4
Small Pivot : 3
4.
연산
→ A가 정렬이 되어 있는 경우 / A가 정렬이 되어 있고 B가 비어있는 경우
먼저 A가 정렬이 되어 있는 경우 atob 내의 프로세스를 수행할 필요가 없다.
수정 하기 전에는 A의 정렬 여부와 상관 없이 무조건 프로세스를 수행하게끔 코드가 작성되어 있었는데, 이 경우 정렬 되어 있는 A에서 피봇을 찾고 연산을 하는 불필요한 과정이 연산 개수를 추가하게 된다.
이에 아이디어를 얻어 예외 케이스에 A가 정렬이 되어 있고 B가 비어 있는 경우도 추가하였다.
이는 무한 루프를 도는 내 코드의 오류를 말끔하게 고쳐주었다.
인자가 2→1→3이 들어왔을 때 1→2→3으로 정렬이 되면 재귀를 멈추어야 한다.
하지만 내 코드는 1→2→3으로 정렬이 되었어도 여기서 또 피봇을 선택하여 정렬을 반복하였다. 따라서 atob 또는 btoa function에 진입하였을 때 예외 처리 시 위와 같은 경우 재귀를 탈출하도록 설계하였다.